Simple Graph Coloring Algorithm
Choose the first color that is not in that. Kempes graph-coloring algorithm To 6-color a planar graph.
 Graph Colouring Computer Science Unplugged Graphing Computer Science Kindergarden
Graph Colouring Computer Science Unplugged Graphing Computer Science Kindergarden
Jan 01 2004 We consider the following game played on a finite graph GLet r and d be positive integers.

Simple graph coloring algorithm. Jan 18 2021 In the following algorithm we will color each vertex in the graph based on this operation. In this article we have explored this wonderful graph colouring article in depth. Feb 01 2021 In this work we give a simple algorithm for 1 epsilonDelta-coloring.
It doesnt guarantee to use minimum colors but it guarantees an upper bound on the number of colors. Graph Coloring is a process of assigning colors to the vertices of a graph. Wigderson Algorithm is a graph colouring algorithm to color any n-vertex 3-colorable graph with On colors and more generally to color any k-colorable graph.
To the third layer etc. We show that we can always color G with Delta1 colors by a simple greedy algorithm. The coloring number colG of a graph G is defined by colG1 min L 6G 2G L.
In the field of distributed algorithms graph coloring is closely related to the problem of symmetry breaking. We use integers 12ldots Delta1 as colors. We use this result to give very easy proofs of the best known.
In a graph no two adjacent vertices adjacent edges or adjacent regions are colored with minimum number of colors. Pick a vertex v_n and list the vertices of G as v_1v_2ldotsv_n so that if i. If the adjacent vertex has color but that color into a bucket set.
Doi101006 jctb19991927 available online at http. This is a slight improvement of the current upper bound of 19. Consider the leftmost graphWhen processing vertices 1 2 3 4 no neighbor has a.
This algorithm makes Oepsilon-12nsqrtn queries which matches the best existing algorithms as well as the classical lower bound for sufficiently large epsilon. Chromatic Number is the minimum number of colors required to properly color any graph. Loop through all its neighbor vertices.
To the second layer red. It is adjacent to at most 5 vertices which use up at most 5 colors from your palette. In this article we will discuss how to find Chromatic Number of any graph.
Jan 01 2000 We prove that the game coloring number and therefore the game chromatic number of a planar graph is at most 18. Wigderson Graph Colouring Algorithm in ONM time. Nov 14 2013 Following is the basic Greedy Algorithm to assign colors.
Put the vertex back. Do a breadth-first search assigning red. On each vertex there will be two extra colors which are possible colors to color the vertex.
Color the rest of the graph with a recursive call to Kempes algorithm. Then go over all the edges and check whether the two endpoints of this edge have different colors. Two players Alice and Bob alternately color the vertices of G using colors from a set of colors X with XrA color αX is a legal color for uncolored vertex v if by coloring v with color α the subgraph induced by all vertices of color α has maximum degree at most d.
Graph coloring is nothing but a simple way of labelling graph components such as vertices edges and regions under some constraints. The chromatic number of a graph G is denoted by G. The basic algorithm never uses more than d1 colors where d is the maximum degree of a vertex in the given graph.
Color first vertex with first color. Basic Greedy Coloring Algorithm. This number is called the chromatic number and the graph is called a properly colored graph.
There is a simple algorithm for determining whether a graph is 2-colorable and assigning colors to its vertices. This is a bipartite graph. We experimentally demonstrate that for most of the tested instances the new algorithm outperforms a recent and very competitive algorithm for decentralized graph coloring in terms of coloring quality.
The fastest randomized algorithms employ the multi-trials technique by Schneider et al. The current state-of-the-art randomized algorithms are faster for sufficiently large maximum degree Δ than deterministic algorithms. To the first layer blue.
In terms of computational complexity - the measure that we computer scientists use to describe. Every planar graph has at least one vertex of degree 5. J dv_iv_n gedv_jv_n that is we list the vertices farthest from v_n first.
Perhaps more importantly we bound the game coloring number of a graph G in terms of a new parameter rG. Aug 02 2010 A simple algorithm for graph coloring is easy to describe but potentially extremely expensive to run. Additionally it can be readily adapted to a quantum query algorithm making tildeOepsilon-1n43 queries.
The vertices of a bipartite graph can be split into two groups such that all neighbors of one group are in the other group. Chromatic number and coloring number. It ensures that no two adjacent vertices of the graph are colored with the same color.
Total coloring algorithm for graphs 1301 with ΔG2 colors using the independent set algorithm. Following Greedy algorithm can be applied to find the maximal edge independent set. This will reduce the complexity on edge coloring.
Jul 25 2016 This paper explores a novel and simple algorithm for decentralized graph coloring that uses a fixed number of colors and iteratively reduces the edge conflicts in the graph.
 1 Graph Theory Brilliant Math Science Wiki Graphing Math Theories
1 Graph Theory Brilliant Math Science Wiki Graphing Math Theories
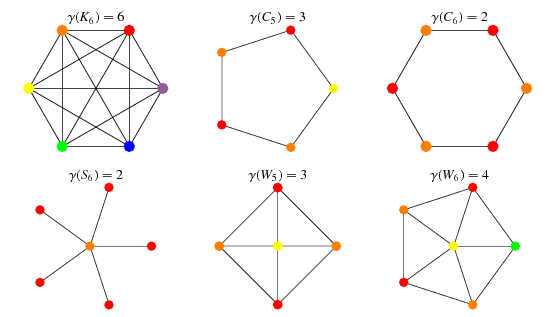 Chromatic Number From Wolfram Mathworld
Chromatic Number From Wolfram Mathworld
![]() Graph Coloring Algorithm Using Backtracking Interviewbit
Graph Coloring Algorithm Using Backtracking Interviewbit
 Graph Coloring Minimum Number Of Colors Beautiful Math For Seven Year Olds Graph Coloring Chromatic Numb In 2020 Coloring Pages Color Graphing Printable Coloring Pages
Graph Coloring Minimum Number Of Colors Beautiful Math For Seven Year Olds Graph Coloring Chromatic Numb In 2020 Coloring Pages Color Graphing Printable Coloring Pages
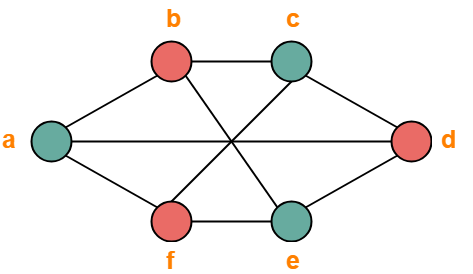 How To Find Chromatic Number Graph Coloring Algorithm Gate Vidyalay
How To Find Chromatic Number Graph Coloring Algorithm Gate Vidyalay
 Graph Coloring Problem Techie Delight
Graph Coloring Problem Techie Delight
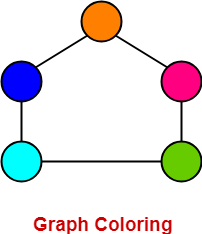 Graph Coloring In Graph Theory Chromatic Number Of Graphs Gate Vidyalay
Graph Coloring In Graph Theory Chromatic Number Of Graphs Gate Vidyalay
 Infographic Timeline Graph Chart Online Documentation And World Statistics Icons Simple Set Sales Diagram S Timeline Infographic Sharing Economy Infographic
Infographic Timeline Graph Chart Online Documentation And World Statistics Icons Simple Set Sales Diagram S Timeline Infographic Sharing Economy Infographic
 Graph Coloring Problem Techie Delight
Graph Coloring Problem Techie Delight
 Graph Coloring Minimum Number Of Colors Luxury International Journal Of Advanced Research And Publication Graphing Color Coloring Pages
Graph Coloring Minimum Number Of Colors Luxury International Journal Of Advanced Research And Publication Graphing Color Coloring Pages
 Graph Coloring Problem Techie Delight
Graph Coloring Problem Techie Delight
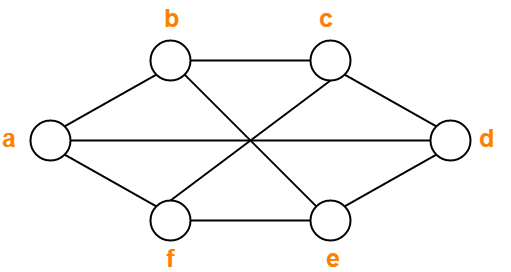 How To Find Chromatic Number Graph Coloring Algorithm Gate Vidyalay
How To Find Chromatic Number Graph Coloring Algorithm Gate Vidyalay
 Add Colors To Your Palette With Color Mixing Viget Bright Color Schemes Brand Color Palette Color Schemes
Add Colors To Your Palette With Color Mixing Viget Bright Color Schemes Brand Color Palette Color Schemes
 Graph Coloring Connect The Dots Graphing Math
Graph Coloring Connect The Dots Graphing Math
Joseph Culberson S Graph Coloring Resources Page
 An Anti Aging Pundit Solves A Decades Old Math Problem Graphing Easy Coloring Pages Love Coloring Pages
An Anti Aging Pundit Solves A Decades Old Math Problem Graphing Easy Coloring Pages Love Coloring Pages
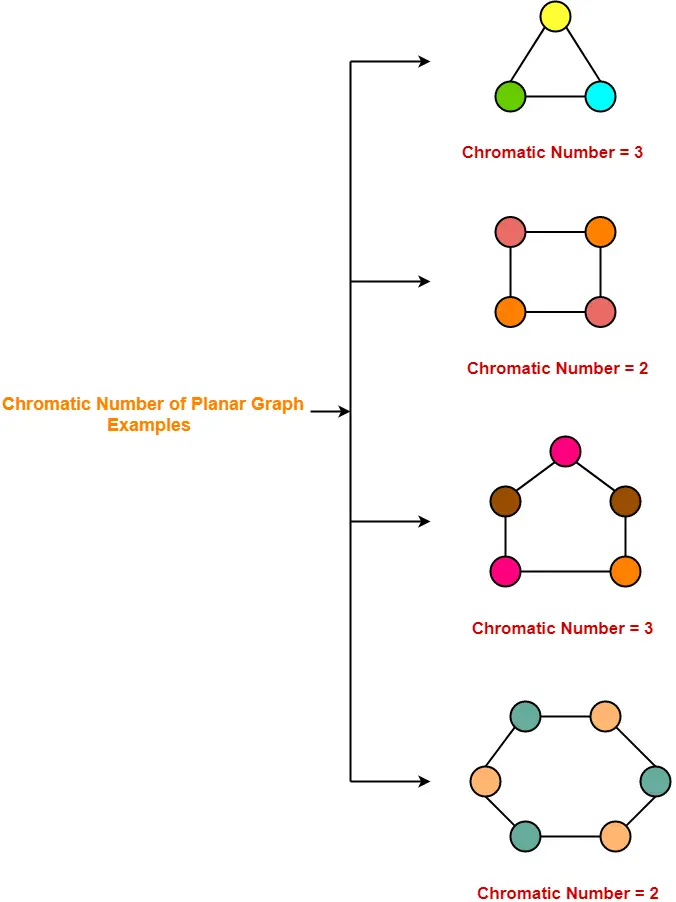 Graph Coloring In Graph Theory Chromatic Number Of Graphs Gate Vidyalay
Graph Coloring In Graph Theory Chromatic Number Of Graphs Gate Vidyalay
 Algorithmic Graph Theory Alan Gibbons Department Of Computer Science University Of Warwick Math Books Teaching Coding Graphing
Algorithmic Graph Theory Alan Gibbons Department Of Computer Science University Of Warwick Math Books Teaching Coding Graphing
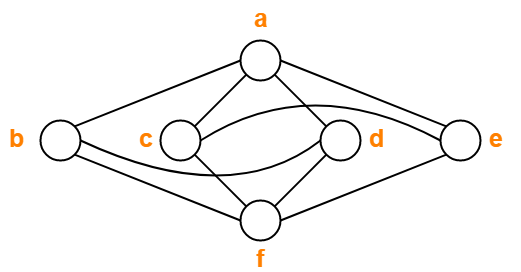 How To Find Chromatic Number Graph Coloring Algorithm Gate Vidyalay
How To Find Chromatic Number Graph Coloring Algorithm Gate Vidyalay